Worm Search
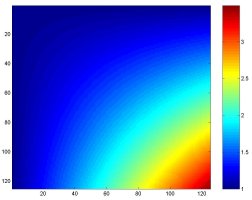
A swarm of intelligent agents search an area for the enemy. At different locations, the agent's sensor range varies. How do we best search? If we use the average detection probability across the field of search, our agents will spend all of their time looking where it is easy to look, i.e. where their sensor range is maximum. This is the "looking under a lamp post" scenario. In order to leverage investigation into more difficult search regions, a sacrifice of accuracy "under the lamp post" must be made. The problem, therefore, calls for tradeoffs on the efficient frontier of optimization. Diminishing returns can emerge. Such is characteristic of Pareto optimization.
Herein are swarm emulations illustrating the high level/uniform coverage tradeoff of such area coverage. The use of the term "worm search" will become apparant upon viewing of the seach dynamics. The process uses disjunctive control - described in detail in CIA publications.
A number of autonomous agents explore a rectangulaly shaped area. Due to environmental changes, each agent's sensing radius changes with position. The detection area, once left, is assumed to decay in confidence ultimately returning to an unsearched status after a period of time. Graphically, as seen in the illustrative MPG's, this resembles a worm.
What, then, is the best search strategy? What objective function do we optimize? One choice is to maximize the average coverage at every point in time. Doing this, however, nudges agents to "search under the lamp post" in regions where their radius of detection is high. This leaves more difficult search regions untouched. Dedicating agent resources to search more difficult regions, though, diminishes the effectiveness of their search in easily searchable regions. There is a clear tradeoff between strong coverage and uniform coverage. As one increases, the other decreases. These examples provide a numerical illustration of this tradeoff.
The agent movement is dictated by disjunctive control. Tuning of the disjuctive components allows illustration of the strong versus uniform tradeoff characteristic of this problem. As parameters are tuned for greater uniformity, strength decreases. As strength increases, uniformity diminishes.
For detailed commentary on the emulation, see the Matlab code provided for each simulation.
- Simple Slope
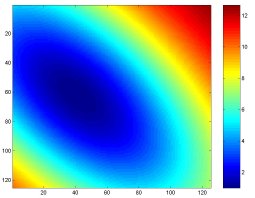
- Guassian Bowl
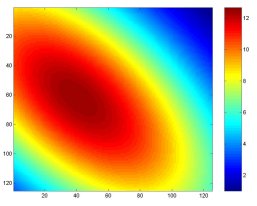
- Guassian Bump
- Homogenous Environment
Sensing Radius is a constant
More Information